How Can You Calculate The Standard Entropy Change For A Reaction From Tables Of Standard Entropies?

Affiliate xviii. Chemical Thermodynamics

Measuring Entropy and Entropy Changes

Jessie A. Key

To gain an understanding of methods of measuring entropy and entropy change.

Equally the temperature of a sample decreases, its kinetic energy decreases and, correspondingly, the number of microstates possible decreases. The third law of thermodynamics states:at absolute naught (0 Chiliad), the entropy of a pure, perfect crystal is zilch. In other words, at absolute zero, there is merely 1 microstate and according to Boltzmann's equation:

$S=k \ln W = k\ln 1=0$

Using this as a reference bespeak, the entropy of a substance can be obtained by measuring the oestrus required to raise the temperature a given amount, using a reversible procedure. Reversible heating requires very slow and very small increases in oestrus.

$\Delta S=\dfrac{q_{\text{rev}}}{T}$

Decide the change in entropy (in J/K) of water when 425 kJ of estrus is applied to it at fifty°C. Assume the modify is reversible and the temperature remains abiding.

Solution

$\Delta\text{S}=\dfrac{q_{\text{rev}}}{T}=\dfrac{425\text{ kJ}}{323.15\text{ K}}=\dfrac{4.25\times10^5\text{ J}}{323.15\text{ K}}=1.32\times 10^5\text{ J/K}$

Standard Tooth Entropy, S°

The standard molar entropy, S°, is the entropy of 1 mole of a substance in its standard state, at ane atm of pressure. These values have been tabulated, and selected substances are listed in Table 18.1a to c "Standard Tooth Entropies of Selected Substances at 298 K".^[1]

Table 18.1a Standard Molar Entropies of Selected Gases at 298 Thousand
Gas	South°[J/(mol·K)]
He	126.2
H₂	130.7
Ne	146.3
Ar	154.8
Kr	164.1
Xe	169.7
H₂O	188.8
N₂	191.half dozen
O_ii	205.2
CO_two	213.viii
I₂	260.seven

Tabular array 18.1b Standard Molar Entropies of Selected Liquids at 298 Grand
Liquid	Due south°[J/(mol·K)]
H₂O	seventy.0
CH₃OH	126.8
Br_two	152.2
CH₃CH₂OH	160.7
C₆H_vi	173.4
CH₃COCl	200.8
C_sixH₁₂ (cyclohexane)	204.iv
C₈H₁₆ (isooctane)	329.3

Tabular array eighteen.1c Standard Molar Entropies of Selected Solids at 298 Thou
Solid	S°[J/(mol·K)]
C (diamond)	2.4
C (graphite)	v.7
LiF	35.7
SiO₂ (quartz)	41.5
Ca	41.6
Na	51.3
MgF₂	57.two
K	64.7
NaCl	72.1
KCl	82.6
I₂	116.one

Several trends emerge from standard molar entropy data:

Larger, more complex molecules have higher standard molar enthalpy values than smaller or simpler molecules. At that place are more possible arrangements of atoms in space for larger, more complex molecules, increasing the number of possible microstates.
Gases tend to take much larger standard molar enthalpies than liquids, and liquids tend to have larger values than solids, when comparing the same or like substances.
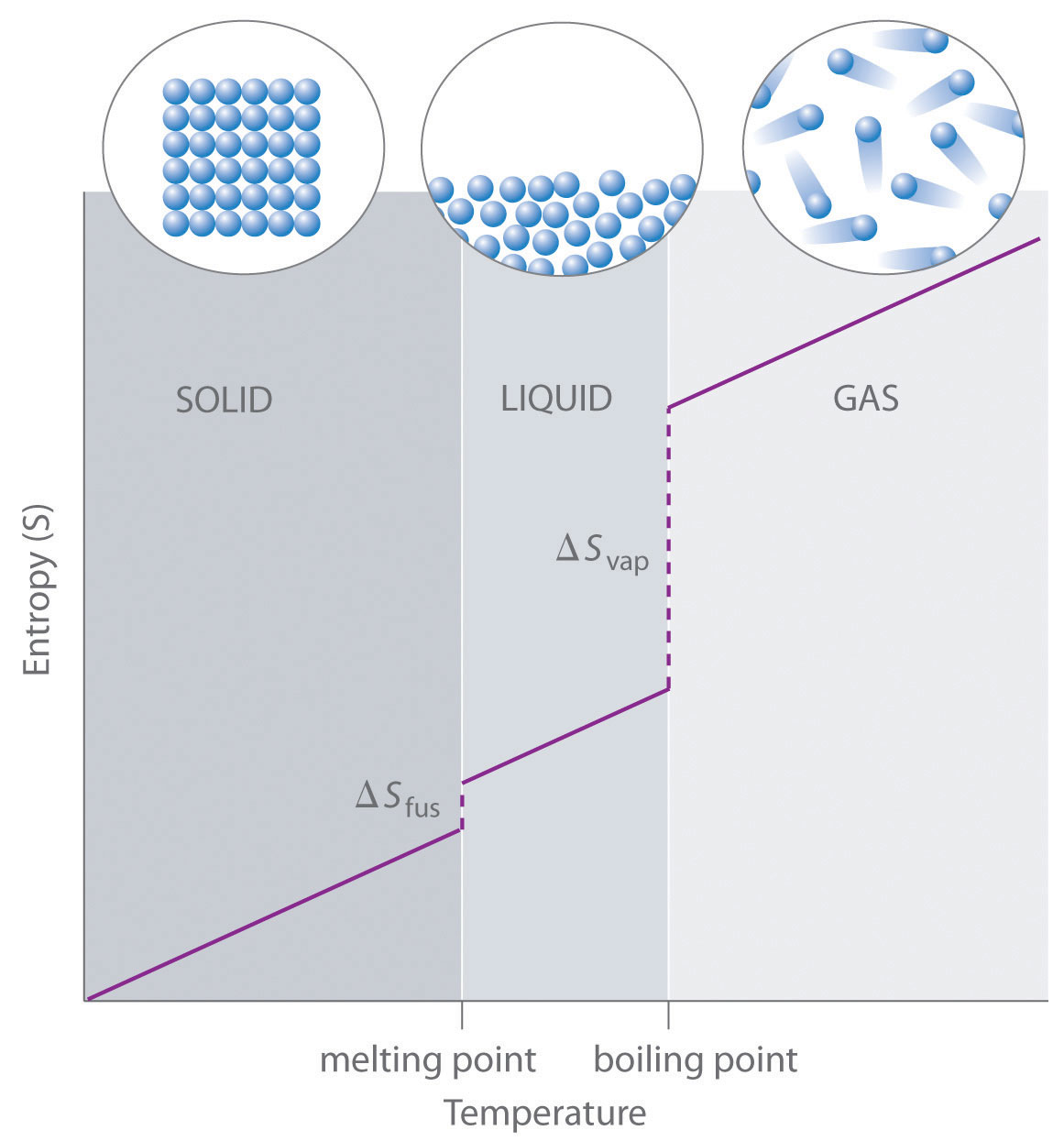
The standard molar entropy of whatever substance increases as the temperature increases. This tin can exist seen in Figure 18.3 "Entropy vs. Temperature of a Single Substance." Big jumps in entropy occur at the stage changes: solid to liquid and liquid to gas. These large increases occur due to sudden increased molecular mobility and larger bachelor volumes associated with the phase changes.

Generalized plot of entropy versus temperature of a single substance. — Figure 18.3 "Entropy vs. Temperature of a Single Substance." This is a generalized plot of entropy versus temperature for a single substance. (Source: UC Davis ChemWiki by University of California\CC-BY-SA-three.0)

Standard Entropy Change of a Reaction, ΔS°

The entropy modify of a reaction where the reactants and products are in their standard country tin exist adamant using the following equation:

$\Delta S^{\circ}=\underset{\text{products}}{\sum nS^{\circ}}-\underset{\text{reactants}}{\sum mS^{\circ}}$

where north and m are the coefficients plant in the balanced chemic equation of the reaction.

Determine the change in the standard entropy, ΔS°, for the synthesis of carbon dioxide from graphite and oxygen:

C(s) + O_two(g) → CO₂(m)

Solution

$\begin{align*} \Delta S^{\circ}&=\underset{\text{products}}{\sum nS^{\circ}}-\underset{\text{reactants}}{\sum mS^{\circ}} \\ &=(213.8\text{ J/mol K})-(205.2\text{ J/mol K}+ 5.7\text{ J/mol K}) \\ &=+2.9\text{ J/mol K} \end{align*}$

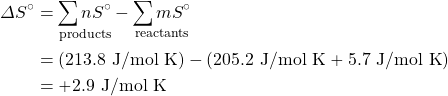
Entropy Changes in the Surroundings

The second constabulary of thermodynamics states that a spontaneous reaction will result in an increase of entropy in the universe. The universe comprises both the organisation existence examined and its surroundings.

$\Delta S_{\text{universe}}=\Delta S_{\text{sys}}+\Delta S_{\text{surr}}$

Standard entropy change can also be calculated by the following:

$\Delta S^{\circ}{}_{\text{universe}}=\Delta S^{\circ}{}_{\text{sys}}+\Delta S^{\circ}{}_{\text{surr}}$

The change in entropy of the surroundings is essentially just a measure of how much energy is being taken in or given off past the system. Under isothermal conditions, we tin can express the entropy change of the surroundings as:

$\Delta\text{S}_\text{surr}=\dfrac{{-q}_{\text{sys}}}{T}\text{ or }\Delta\text{S}_\text{surr}=\dfrac{-\Delta H_{\text{sys}}}{T}\hspace{1em}\text{(at constant pressure)}$

For the previous example, the modify in the standard entropy, ΔSouth°, for the synthesis of carbon dioxide from graphite and oxygen, utilize the previously calculated ΔSouth°_sys and standard enthalpy of formation values to make up one's mind S°_surr and ΔS°_universe.

Solution

Start nosotros should solve for the ΔH°_sys using the standard enthalpies of formation values:

$\begin{align*} \Delta H^{\circ}{}_{\text{sys}}&=\Delta H^{\circ}{}_{\text{f}}[\ce{CO2(g)}]-\Delta H^{\circ}{}_{\text{f}}[\ce{C(s)}+\ce{O2(g)}] \\ &=(-393.5\text{ kJ/mol})-(0\text{ kJ/mol}+0\text{ kJ/mol}) \\ &=-393.5\text{ kJ/mol} \end{align*}$

Now we can catechumen this to the ΔDue south°_surr:

$\Delta S^{\circ}{}_{\text{surr}}=\dfrac{-\Delta H_{\text{sys}}}{T}=\dfrac{-393.5\text{ kJ/mol}}{298\text{ K}}=-1.32\text{ kJ/mol K}$

Finally, solve for ΔSouth°_universe:

$\begin{align*} \Delta S^{\circ}{}_{\text{universe}}&=\Delta S^{\circ}{}_{\text{sys}}+\Delta S^{\circ}{}_{\text{surr}} \\ &=(+2.9\text{ J/mol K})+(-1.32\times 10^3\text{ J/mol K}) \\ &=-1.3\times 10^3\text{ J/mol K} \end{align*}$

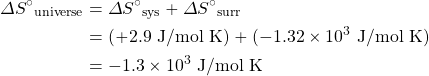
At absolute goose egg (0 M), the entropy of a pure, perfect crystal is nothing.
The entropy of a substance can be obtained by measuring the heat required to raise the temperature a given corporeality, using a reversible process.
The standard molar entropy, S°, is the entropy of 1 mole of a substance in its standard state, at one atm of pressure.

Source: https://opentextbc.ca/introductorychemistry/chapter/measuring-entropy-and-entropy-changes/

Posted by: combsobjer1979.blogspot.com

How Can You Calculate The Standard Entropy Change For A Reaction From Tables Of Standard Entropies?

Measuring Entropy and Entropy Changes

Standard Tooth Entropy, S°

Standard Entropy Change of a Reaction, ΔS°

Entropy Changes in the Surroundings

0 Response to "How Can You Calculate The Standard Entropy Change For A Reaction From Tables Of Standard Entropies?"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel